Michaelis–Menten Enzyme Kinetics
1D Ordinary Differential Equations
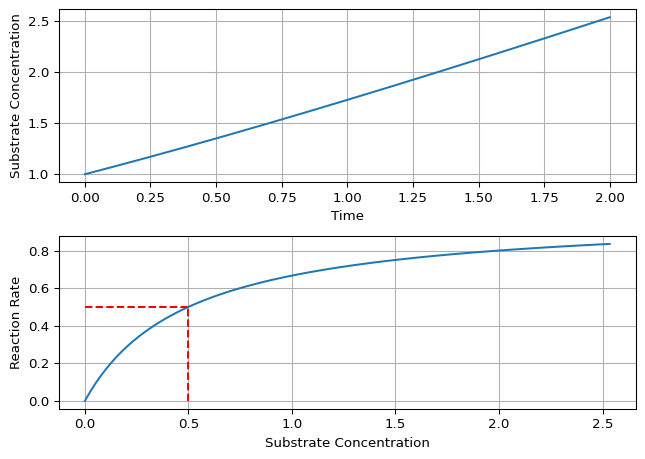
Michaelis–Menten kinetics is a foundational model in biochemical reaction dynamics. It relates substrate concentration to reaction rate using a saturating nonlinearity.
The (simplified) substrate dynamics implemented in the reference script is:
\[ \dot s = \frac{V_{\max}s}{K_m + s} \tag{1}\]
where \(V_{\max}\) is the maximum rate and \(K_m\) is the Michaelis constant.
Reference Implementation
See:
amlab/odes_1d/michaelis_menten.py
The helper plot_michaelis_menten(...) produces:
- \(s(t)\) over time
- \(v(s)\) with guides at \(s=K_m\) and \(v=V_{\max}/2\)
Render-time Figure

Exploration
- Increase \(V_{\max}\) and observe how the rate curve changes.
- Increase \(K_m\) (lower affinity). How does the saturation point shift?
Run Locally
python amlab/odes_1d/michaelis_menten.py