scipy.integrate.solve_ivp() and matplotlib.
2D Ordinary Differential Equations
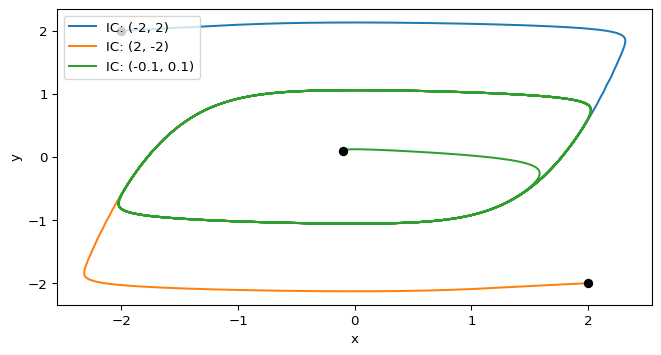
The Van der Pol oscillator is a prototypical nonlinear system that exhibits self-sustained oscillations. For a wide range of initial conditions, trajectories converge to a stable limit cycle.
In the form we will use in this course, the system is written as (Strogatz 2024, chap. 7.5):
\[\begin{aligned} \dot x &= \mu\,(y - f(x)) \\ \dot y &= -\frac{x}{\mu} \end{aligned} \tag{1}\]
where \(\mu>0\) controls the strength of the nonlinearity (and the fast–slow character for large \(\mu\)), and
\[ f(x) = \frac{x^3}{3} - x. \tag{2}\]

scipy.integrate.solve_ivp() and matplotlib.
Follow the steps outline in the CDIMA model to explore how the Van der Pol system behaves for different initial conditions and parameters.
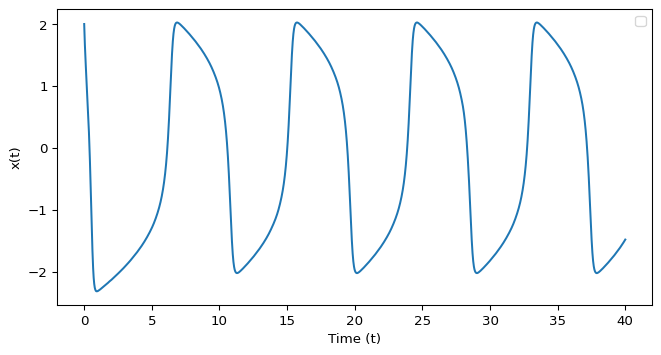
The Van der Pol system has a stable limit cycle that attracts trajectories from a wide range of initial conditions. Plot this limit cycle as a \(x(t)-t\) plot, and verify that it matches the phase plane trajectories.
/tmp/ipykernel_3216/2854713749.py:14: UserWarning:
No artists with labels found to put in legend. Note that artists whose label start with an underscore are ignored when legend() is called with no argument.
scipy.integrate.solve_ivp() and matplotlib.
The amplitude and period of the limit cycle depend on \(\mu\). There are two phases of the limit cycle: a slow phase where trajectories move slowly near the cubic nullcline, and a fast phase where trajectories rapidly jump between branches of the nullcline. The speed of the slow phase increases with \(\mu\), while the fast phase becomes more abrupt. This leads to a characteristic “relaxation oscillation” shape for large \(\mu\).
Play with the parameter \(\mu\) to see how it changes the shape of the limit cycle and the transient dynamics.