scipy.integrate.solve_ivp() and matplotlib.
2D Ordinary Differential Equations
The FitzHugh–Nagumo model is a simplified neuron model that captures key features of excitability and spiking behavior. It consists of two coupled ODEs:
\[\begin{aligned} \epsilon \dot v &= f(v) - w + I_{\text{app}} \\ \dot w &= v - \gamma w \end{aligned} \tag{1}\]
Where \(v\) is the fast variable representing the membrane potential, \(w\) is a recovery variable, \(I_{\text{app}}\) is an applied current, and \(\epsilon \ll 1\) controls the timescale separation between the fast variable \(v\) and the slow variable \(w\). \(f(v)\) is a cubic nonlinearity, often taken as
\[ f(v) = v (1 - v)(v - \alpha),\quad \text{for } 0 < \alpha < 1 \tag{2}\]

scipy.integrate.solve_ivp() and matplotlib.
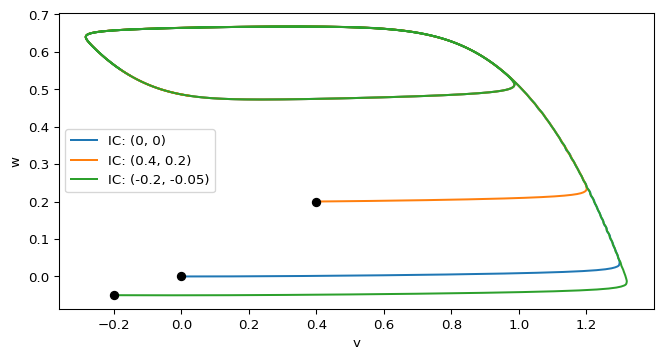
Follow the steps outline in the CDIMA model to explore how the FitzHugh–Nagumo system behaves for different initial conditions and parameters.
In the excitable regime, trajectories typically stay near the resting equilibrium, but sufficiently large perturbations can trigger a large excursion (a “spike”) before returning to rest.
Below we plot the fast variable \(v(t)\) for a fixed parameter set and initial condition.
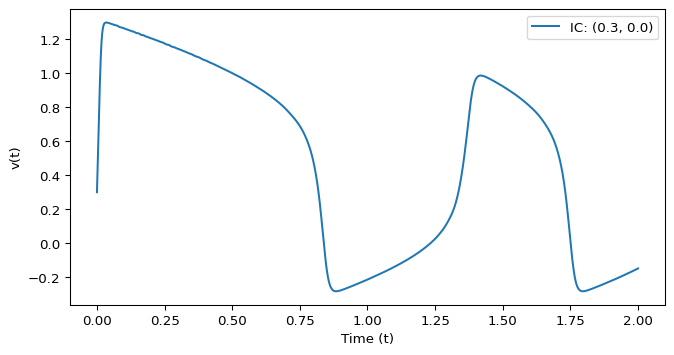
Try changing the initial condition and parameters to see how the time series changes. What regimes of behavior do you observe? Can you connect these observations to the phase plane trajectories and the underlying theory of excitability?